Online-Dreiecksflächenrechner
Kostenloser Dreiecksflächenrechner online in verschiedenen Methoden.
ErklärungBerechnen Sie die Fläche eines beliebigen Dreiecks in Sekunden mit dem Dreiecksflächenrechner
Haben Sie Schwierigkeiten bei der Berechnung der Dreiecksfläche?
Mit dem Dreiecksflächenrechner können Sie:
* Die Fläche eines beliebigen Dreiecks schnell und einfach berechnen.
* Die Längen der Seiten oder die Basis und Höhe eingeben.
* Das Ergebnis in den bevorzugten Einheiten erhalten.
* Die Lösungsschritte anzeigen, um zu erfahren, wie man die Fläche berechnet.
Das Tool ist sehr einfach zu bedienen:
* Besuchen Sie einfach unsere Website.
* Geben Sie die Längen der Seiten oder die Basis und Höhe ein.
* Klicken Sie auf "Berechnen".
* Die Fläche des Dreiecks wird sofort angezeigt.
Probieren Sie noch heute den Dreiecksflächenrechner aus!
Mit diesem Tool können Sie die Dreiecksfläche auf drei verschiedene Arten berechnen: durch drei Seiten, durch zwei Seiten und den eingeschlossenen Winkel, durch Basis und Höhe, oder durch zwei Winkel und die eingeschlossene Seite. Dieses Tool ist kostenlos ohne Gebühren.
Wie berechnet man die Fläche eines Dreiecks?
Schritt1 : Um die Fläche eines Dreiecks zu berechnen, müssen Sie die passende Methode basierend auf der Form des Dreiecks oder den verfügbaren Daten auswählen. Es gibt mehrere Methoden, wie die Berechnung mit drei Seiten, zwei Seiten und dem eingeschlossenen Winkel, Basis und Höhe, oder zwei Winkel und der eingeschlossenen Seite.
Schritt2 : Wählen Sie die passende Methode und geben Sie die Daten in die vorgesehenen Felder ein.
Schritt3 : Klicken Sie auf Berechnen, um die Fläche des Dreiecks zu erhalten.
Merkmale des Dreiecksflächenrechners
* Die Fläche eines beliebigen Dreiecks schnell und einfach berechnen.
* Die Längen der Seiten oder die Basis und Höhe eingeben.
* Das Ergebnis in den bevorzugten Einheiten erhalten.
* Die Lösungsschritte anzeigen, um zu erfahren, wie man die Fläche berechnet.


Eine Reise in die Welt der Dreiecke: Entdecken der Geheimnisse der Flächenberechnung
In diesem Artikel werden wir in eine Reise eintauchen, um die Geheimnisse der Berechnung der Dreiecksfläche mit verschiedenen Methoden zu entdecken.
Was ist die Fläche eines Dreiecks?
Die Fläche eines Dreiecks ist der Bereich, der innerhalb seiner drei Seiten eingeschlossen ist. Sie wird in Flächeneinheiten gemessen, wie Quadratcentimeter oder Quadratmeter.
Methoden zur Berechnung der Dreiecksfläche:
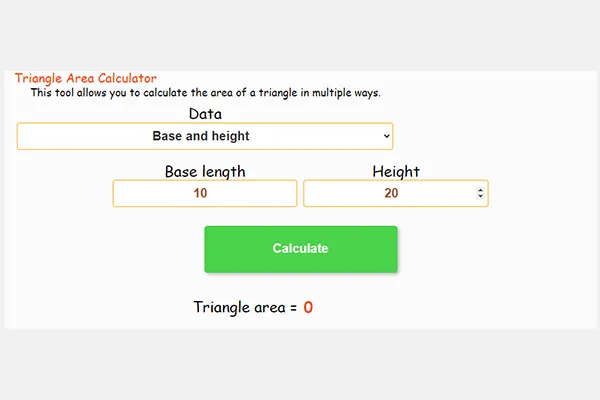
1. Methode Fläche = ½ × Basis × Höhe:
* Erklärung der Methode: Diese Methode basiert auf der Unterteilung des Dreiecks in ein Rechteck mit derselben Basis und Höhe. Sie wird bei rechtwinkligen Dreiecken verwendet, bei denen eine Seite die Basis und die andere senkrecht dazu die Höhe ist.
* Flächenformel: Fläche des Dreiecks = ½ × Basis × Höhe
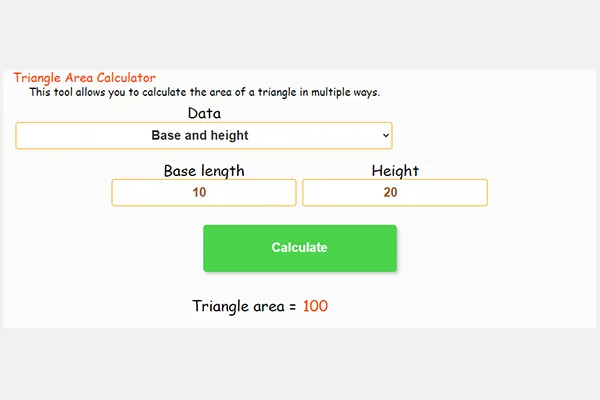
* Beispiel: Angenommen, wir haben ein rechtwinkliges Dreieck mit einer Basis von 10 cm und einer Höhe von 5 cm.
Wie groß ist seine Fläche?
Fläche des Dreiecks = ½ × 10 cm × 5 cm = 25 cm²
"Dreiecke sind eine der wichtigsten grundlegenden geometrischen Formen und spielen eine wichtige Rolle in vielen Bereichen wie Mathematik, Ingenieurwesen und Physik."– Plattru