Online Triangle Area Calculation Tool
Free Online Triangle Area Calculator with Multiple Methods.
ExplanationWith the Triangle Area Tool, calculate the area of any triangle in seconds!
Having trouble calculating triangle areas?
With the Triangle Area Tool, you can:
* Calculate the area of any triangle quickly and easily.
* Enter the side lengths or base and height values of the triangle.
* Get the result in your preferred units.
* View solution steps to understand how the area is calculated.
The tool is very easy to use:
* Just visit our website.
* Enter the side lengths or base and height values of the triangle.
* Press the "Calculate" button.
The triangle area will be displayed instantly.
Try the Triangle Area Tool today!
This tool allows you to calculate the triangle area using three different methods:
1. Using three sides
2. Using two sides and the included angle
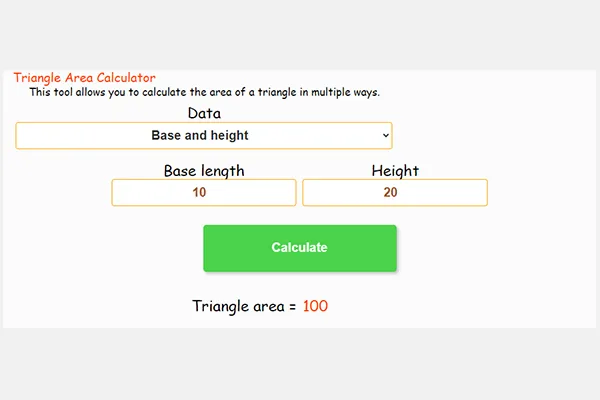
3. Using base and height
4. Using two angles and the included side.
This tool is free to use without any charges.
How to calculate triangle area?
Step1 :
To calculate the area of a triangle, select the appropriate method based on the triangle type or the data you have.
Methods include using three sides, two sides and an included angle, base and height, or two angles and the included side.
Step2 :
Choose the appropriate method and enter the data in the designated fields.
Step3 :
Press "Calculate" to get the area of the triangle.
Features of the Triangle Area Tool
* Calculate the area of any triangle quickly and easily.
* Enter the side lengths or base and height values of the triangle.
* Get the result in your preferred units.
* View solution steps to understand how the area is calculated.


Journey through Triangles: Discovering the Secrets of Area Calculation
In this article, we will dive into the secrets of calculating triangle areas using different methods.
What is the area of a triangle?
The area of a triangle is the space enclosed within its three sides. It is measured in units of area, such as square centimeters or square meters.
Methods of calculating triangle area:
1. Area = ½ × base × height:
* Explanation: This method is based on dividing the triangle into a rectangle with the same base and height. It is used for right-angled triangles where one side is the base and the other is the height.
* Area formula: Triangle area = ½ × base × height
* Example: Suppose we have a right-angled triangle with a base of 10 cm and a height of 5 cm. What is its area?
Triangle area = ½ × 10 cm × 5 cm = 25 cm²
2. Area = (1/2) × side × side × sine of the included angle:
* Explanation: This method uses the sine of the included angle between two sides to calculate the triangle's area. It works for any type of triangle—right-angled, acute, or obtuse.
* Area formula: Triangle area = (1/2) × side × side × sine of the included angle
* Example: Suppose we have a triangle with sides of 6 cm and 8 cm, and the sine of the included angle between them is 0.4.
What is its area?
Triangle area = (1/2) × 6 cm × 8 cm × 0.4 = 9.6 cm²
3. Area = √(s(s-a)(s-b)(s-c)):
* Explanation: This method uses Heron's formula to calculate the area. Where s is the semi-perimeter of the triangle, and a, b, and c are the lengths of its sides.
* Area formula: Triangle area = √(s(s-a)(s-b)(s-c))
* Example: Suppose we have a triangle with sides of 6 cm, 8 cm, and 10 cm. What is its area?
First, calculate the semi-perimeter: s = (6 cm + 8 cm + 10 cm) / 2 = 12 cm.
Second, calculate the triangle area:
Triangle area = √(12 cm (12 cm - 6 cm) (12 cm - 8 cm) (12 cm - 10 cm)) = 9.6 cm²
Tips for calculating triangle areas:
* Identify the triangle type: It is important to identify the type of triangle (right-angled, acute, or obtuse) to choose the appropriate method for calculating the area.
* Ensure data accuracy: Make sure the triangle side lengths and angles are measured correctly.
" Triangles are one of the most important basic geometric shapes and play a crucial role in many fields, such as mathematics, engineering, and physics. "– Plattru