온라인에서 무료로 사각형 면적 계산기
빠르고 정확한 사각형 면적 계산기, 복잡한 계산과 수학적 실수를 없애세요.
설명사각형 면적 계산기로 계산을 창의적으로 해보세요!
사각형의 면적을 수작업으로 계산하는 데 어려움을 겪고 있나요? 복잡한 계산과 숫자에 고민하지 마세요. 사각형 면적 계산기는 정확하고 빠른 결과를 제공합니다.
사각형 면적 계산기란?
사각형의 면적을 간단하고 빠르게 계산할 수 있도록 도와주는 스마트한 도구입니다. 사각형의 길이와 너비를 입력하면 즉시 결과를 얻을 수 있습니다.
이 도구가 필요한 이유는?
* 높은 정확도: 100% 정확한 결과를 얻을 수 있습니다. 계산 실수는 이제 그만.
* 빠른 계산: 번거로운 수작업 계산에서 벗어나세요.
* 사용 용이성: 누구나 사용할 수 있는 직관적인 인터페이스.
* 시간과 노력 절약: 더 중요한 일에 시간을 투자하세요.
* 모든 사람에게 적합: 학생, 엔지니어, 인테리어 디자이너, 집 수리 중이신 분 모두에게 유용합니다.
도구 사용 방법
* 길이 값을 입력하세요.
* 너비 값을 입력하세요.
* "계산" 버튼을 클릭하세요.
* 즉시 정확한 결과가 표시됩니다.
데이터 준비
사각형 면적과 둘레 계산 방법
단계1 : 사각형 면적을 계산하려면 두 면의 길이를 입력해야 합니다.
단계2 : 정해진 입력란에 데이터를 입력하세요.
단계3 : 입력을 완료한 후 계산을 클릭하여 사각형 면적을 얻으세요.
사각형 면적 계산기의 용도
* 수학적 계산: 다른 도형의 면적 계산에도 사용됩니다.
* 인테리어 디자인: 벽과 바닥의 면적을 계산하여 필요한 자재를 결정합니다.
* 건축: 건설 비용을 추정하기 위해 표면과 바닥 면적을 계산합니다.
* 목재와 금속 작업: 금속 및 목재 패널의 면적을 계산합니다.
사각형 면적: 개념, 계산 및 응용
사각형은 네 개의 직각(90도)과 맞은편 두 변이 같은 길이를 가진 2D 도형입니다.
사각형 면적이란?
사각형 면적은 사각형이 평면에서 차지하는 면적을 나타냅니다. 즉, 사각형의 경계 안에 있는 영역입니다.
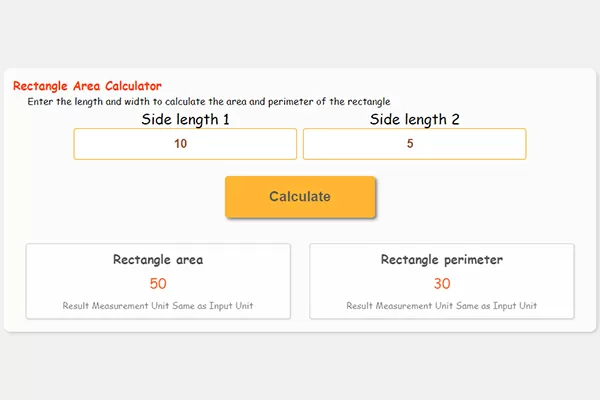
사각형 면적 계산 방법
공식:
사각형 면적 = 길이 × 너비
예시:
길이가 5cm이고, 너비가 3cm인 사각형의 면적은:
면적 = 5cm × 3cm = 15cm²
면적 단위:
사각형 면적은 제곱 센티미터(cm²), 제곱미터(m²), 제곱킬로미터(km²) 등으로 측정됩니다.
사각형 면적을 계산하는 이유
사각형 면적을 계산하는 것은 일상생활과 여러 분야에서 유용합니다:
* 건설: 벽, 바닥, 지붕에 필요한 자재 양을 계산합니다.
* 농업: 농지 면적을 계산하고 생산량을 결정합니다.
* 인테리어 디자인: 방의 면적을 계산하여 필요한 가구 크기를 정합니다.
* 과학: 물리학과 화학에서 여러 방정식과 법칙에 면적 계산이 사용됩니다.
사각형 면적 계산 예시:
* 바닥 면적 계산: 방 바닥에 카펫을 깔려면 바닥 면적을 계산해야 합니다.
* 벽 면적 계산: 벽을 칠하려면 면적을 계산하여 필요한 페인트 양을 정합니다.
* 종이 면적 계산: 종이에 이미지를 인쇄하려면 면적을 계산하여 이미지가 맞는지 확인합니다.
인용문"사각형 면적 계산은 수학에서 중요한 기본 기술로, 일상 생활에서 실용적인 많은 응용이 있습니다. 면적 개념과 계산법을 이해하면 다양한 문제를 쉽게 해결할 수 있습니다."– Plattru